全細孔容積
全ての細孔の容積の総和を全細孔容積(Total Pore Volume)といいます。全細孔容積は、比表面積と共に多孔体の重要な物性のひとつです。但し、全細孔容積といってもいくつかの考え方があります。ここではその考え方の違いをご紹介します。
|
| (1) |
1点法全細孔容積
相対圧が1に充分近い状態、すなわち飽和蒸気圧付近の圧力では、吸着ガスが殆どの細孔内に液相状態で存在すると考えられます。言い換えれば、細孔内で毛管凝縮現象が起こっています。したがって、このときの吸着ガスの量を液体換算すれば、全細孔容積を求めることができます。この値には、“細孔形状の仮定”は含まれません。
ここで含まれる細孔の大きさ(細孔径)の上限は、計算に使用する相対圧の値に依存します。良く使用される液体窒素温度での窒素ガス吸着の場合は以下のようになります。
ここでは細孔形状を円筒形と仮定しています。
| |
相対圧0.931 |
: |
直径約30nmの細孔まで |
| |
相対圧0.96 |
: |
直径約50nmの細孔まで |
| |
相対圧0.98 |
: |
直径約98nmの細孔まで |
| |
相対圧1.00 |
: |
直径∞
|
全細孔容積計算に使用する相対圧をむやみに大きくすると、吸着等温線の勾配が大きく変化するところになり、その結果ばらつきが大きくなるので注意が必要です。
この方法は、測定ポイントが1点だけです。考え方がシンプルで仮定が少ないことが特徴です。そのかわり細孔分布に関する情報は含まれていません。
|
| (2) |
BJH法、MP法などの細孔分布計算結果から得られる細孔容積の積算値=全細孔容積
ここでの全細孔体積は、細孔分布計算を行った範囲の細孔が対象となります。また、細孔形状もその計算手法に大きく依存します。例えばBJH法の場合は、細孔形状が円筒形であるという仮定に基づいています。
つまり、1回の吸着等温線測定から、複数種類の“全細孔容積”が計算できることになります。これらの値を運用したり評価する場合には、上記1)と2)のどちらを採用するのか、どちらの値が使用されているのか、 などについて明らかにしておく必要があります。
|
|
平均細孔直径(4V/A)
細孔構造に関していろいろな表現法がありますが、そのひとつに“平均細孔直径(4V/A)”というものがあります。これは、ある種の代表径を意味し、比表面積(A)と全細孔容積(V)の2つの物性値のみから計算できるものです。
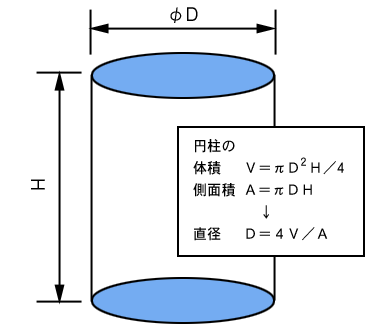
この代表径は、全ての細孔をひとつの(大きな)円筒形細孔で代表させて考えます(下図)。大きなひとつの円筒形細孔は、体積V、表面積A(側面積)を持っています。円筒形ですから、VとAはそれぞれ次式で決めることができます。
 |
体積 |
|
V=πD2H/4 |
| |
側面積 |
|
A=πDH |
この2つの式からHを消去すると次の式が得られます。
 |
直径D=4V/A |
ここで もとめられたDのことを、“平均細孔直径(4V/A)”と呼びます。 |
 |
“全ての細孔ををひとつの(大きな)円筒形細孔で代表させる”という少し乱暴な方法ですので、細孔分布のモード径やメディアン径などとは異なります。
ただ、比表面積と全細孔容積を、それぞれBET1点法と1点法全細孔容積を採用すれば、吸着等温線のわずか2個の測定点だけで求めることができますので、測定は簡単になります。しかも、系全体の特徴を示していることが多いので、昔から良く利用されています。 |
 |

