フーリエ変換とアポダイゼーション
インターフェログラム
FTIRを使用して試料を測定する際,通常,測定モードを透過率または吸光度に設定します。しかし,FTIRは分散型の分光光度計とは異なり,これらのスペクトルは直接測定されるものではありません。
光源を出た赤外光は,光路の途中でマイケルソン干渉計を通ります。マイケルソン干渉計はビームスプリッタ,移動鏡,固定鏡で構成され,ビームスプリッタで2つに分割された光は移動鏡と固定鏡で反射されてビームスプリッタで再度合成されます。移動鏡が往復運動すると固定鏡との間で光路差が生じるために,位相差が時間的に変化する2つの光を合成した干渉光がマイケルソン干渉計で得られます。この干渉光の強度を,横軸を光路差として記録したものがインターフェログラムです。
FTIRにより直接取得されるデータは,試料を透過してきた赤外光を記録したこのインターフェログラムですが,これを見ても試料の特性はわかりません。横軸が波数(波長)となった通常のスペクトルを得るためには,コンピュータによるフーリエ変換という処理が必要となります。このことは直接スペクトルが得られる分散型の分光光度計とは異なり,FTIRの大きな特徴となっています。
フーリエ分光の原理
試料を測定して最終的に欲しいデータは,前節にありますように横軸を波数にとったスペクトルです。そもそもスペクトルとは,さまざまな波長の光が混合した光を分解して,波長ごとの強度をプロットしたもので,この分解作業を分光と呼びます。
波長λの赤外光がマイケルソン干渉計に入射すると,分割された2つの光路長の差(光路差)が整数倍のとき波の山と山・谷と谷が重なるので2つの光が強めあい,半整数倍(整数+1/2倍)のときは逆に弱めあうことになります。もとの光の強度をP(λ)とすると,光路差xのときの強度I(x)は
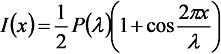
と表すことができます。実際のフーリエ変換では上式の交流成分(cosの項)が波長λの赤外光に対してできるインターフェログラムということになります。
実際には光源から出た光はいろいろな波長の光を合成したものなので,得られるインターフェログラムは上式をいろいろなλについて足し合わせたものとなります。光路差が0となるときは,すべての波長について光が強めあうことになるので,インターフェログラムは高い強度を示します。これをセンターバーストと呼んでいます。
さて一般に,いろいろな周期を持つ波を足し合わせたものから,各周期の波の強度を算出するのがフーリエ変換という操作です。そのフーリエ変換を,インターフェログラムに用いれば各周期つまり波長ごとの強度を得ることができるわけです。
波長λの代わりに波数νを使い,連続的な波数の赤外光からインターフェログラムI(x)がつくられるとすると,I(x)は,
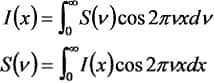
のように表すことができます。ここでS(ν)は波数νにおける赤外光の強度です。
フーリエ変換の手法を用いると,とS(ν)が計算できます。このようにして得られたデータがパワースペクトルであり,バックグラウンドとサンプルのパワースペクトルの比をとったものが透過率で表したスペクトルです。
アポダイゼーション
以上のように,測定されたインターフェログラムをフーリエ変換することにより,最終的には透過率(あるいは吸光度に変換した)スペクトルを得ることができます。
ただし,前節の記述は理論的なものであり,実際の測定は理想的な状態とは異なります。
特に,ご覧の通り上式の積分範囲は0から無限大となっていますが,これは移動鏡の動く範囲が無限の長さであることに対応しています。このような動作は不可能であり,移動鏡は有限の長さを往復するだけなので,実際にはこの積分は有限の範囲で打ち切らざるを得ないことになります。
例えば,積分を有限の範囲[-L,L]で打ち切り,その範囲外の寄与を計算に入れないものとすると,フーリエ変換の式は
と書くことができます。ただし,
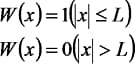
です。
この計算は,得られるスペクトルS(ν)にどのような影響を与えるでしょうか。S(ν)には,関数W(x)のフーリエ変換による像が畳み込まれます。W(x)のフーリエ変換像は
となり,大きなピークの周りに,リップル(波打つような小さなピークの重なり)が発生したものになります。
矩形波W(x)とw(ν)
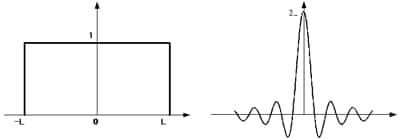
このw(ν)をスペクトルS(v)に畳み込むと,スペクトル中のピークの周りに,W(x)にあるようなリップルが発生することになります。上記のような単純な矩形波(W(x))の場合はピークの次に大きい最大のリップルは,ピークの隣の谷であり,深さはピーク高さの約21%となります。リップルが大きいと,得られるスペクトルが,ピーク類似の凹凸が見られる実際とは異なったものになってしまいます。
一方,積分範囲の途中で単純に計算を打ち切る形の矩形波のかわりに,
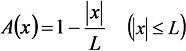
のような三角波を上記のW(x)の代わりにとして採用すると,フーリエ変換像a(ν)は
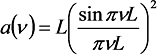
となります。
三角波A(x)とa(ν)
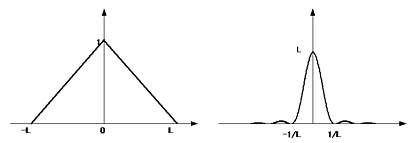
一見してリップルが小さくなっています。これは積分を範囲の端で突然打ち切るのではなく,端に近くなるにつれて一定の割合で寄与を減らしていくようにしたことの効果です。ただし,中心のピークが低くなってしまい,またその幅も若干広がっております。これは実際のスペクトルでは分解能の低下として現れます。
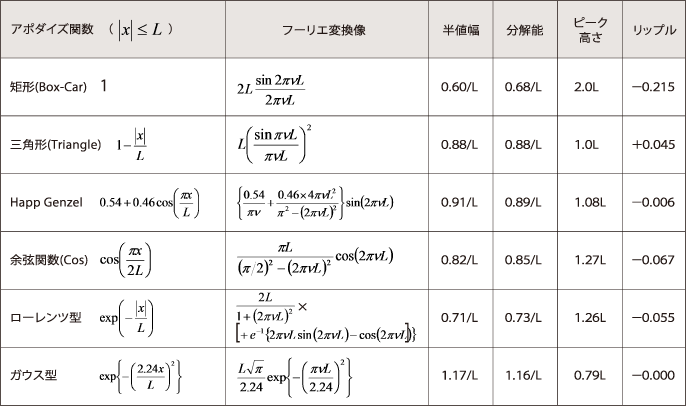
この例のように,フーリエ変換の積分にある種の関数を掛けてリップルを小さくすることをアポダイゼーションと呼び,関数をアポダイズ関数と呼びます。矩形波と三角波の例から想像されるように,リップルを小さくすることと,分解能・ピークの高さはトレードオフの関係にあり,一方を良くするともう一方が悪化します。従って目的に応じてアポダイズ関数を選択する必要があります。
リップルの大きさや分解能などの兼ね合いから,通常よく使われるのがHapp-Genzel関数
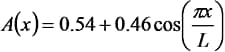
で,フーリエ変換像は
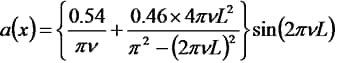
となります。
Happ-Genzel A(x)とa(ν)
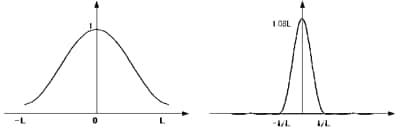
フーリエ変換像を見ると,中央のピークも高く,リップルも良く抑えられているのがわかります。
通常はこのHapp-Genzel関数を使うことが多いのですが,特に分解能を必要とするガス測定などの場面では,矩形(Box-Car)関数を使用します。
このように,アポダイズ関数は目的に応じた使い分けをすることが必要です。