多変量解析を用いたミネラルウォーターの分析事例
近年,化学計測分野では混合成分の定量や多数試料の分類を目的として多変量解析が多く用いられるようになっています。多変量解析を用いることで,混合試料中の目的成分の量を簡便に求めたり,また多くの試料を分類したりすることができます。今回,ミネラルウォーターが紫外領域で特有の吸収スペクトルを与えることを利用し,多変量解析を用いた各種分析を行いましたので紹介いたします。
1. 多変量解析の全体像
多変量解析とは多数のデータからなる分析データを統計的に解析する手法のことであり,旧来の解析手法では得られなかった情報を得ようとするものです。とくに化学計測分野で用いられる場合は,”ケモメトリックス”と呼ばれる場合もあります。
多変量解析は様々な手法から成りますが,大きく定量手法と分類手法に分かれます。
定量手法には重回帰法(MLR またはILS),PCR,PLS 等があります(1)。これらを用いると多成分混合試料における各成分(あるいは目的成分)の量を求めることができます。重回帰法では分析者が特定のデータ(説明変数)を選択する必要がありますが,PCR,PLS ではその必要はなく全データを利用することができます。またPCR,PLSは重回帰法に比べてノイズ(データのふらつき)の影響を受けやすいという一面を持っています。
分類手法には主成分分析(PCA),クラスター分析,判別分析,因子分析等があります(2)。これらを用いることで多数試料を類似度に基づいて分類しその特徴を把握したり,産地の判別に役立てたりすることが可能となります。多変量解析の全体像をまとめると図1のようになります。
今回は,定量手法の中から重回帰法を,分類手法の中から主成分分析(PCA)とクラスター分析を選び,それらを用いて解析しました。

図1. 多変量解析の全体像
| (1) | MLR | : Multiple Linear Regression |
| ILS | : Inverse Least Squares | |
| PCR | : Principal Component Regression | |
| PLS | : Partial Least Squares | |
| (2) | PCA | : Principal Component Analysis |
2. 重回帰法を用いたミネラルウォーター混合試料の同時定量
重回帰法を用いることで多成分混合試料における各成分(あるいは目的成分)の量を求めることができます。今回,市販のミネラルウォーター3 種A,B,C が様々な割合で混合された試料に対し,重回帰法を用いて各試料における混合比を求めました。
はじめに混合比を変えた標準試料を用意し検量モデルを作成した後,混合比既知の検証用試料を用意して検量モデルの検証を行いました。
標準試料9 点と検証用試料3 点に対し紫外可視近赤外分光光度計UV-3600 を使用して紫外領域の吸収スペクトルを測定しました。光路長10 mm の石英セルを用い,イオン交換水を基準として測定したミネラルウォーターA,B,C の各吸収スペクトルを図2 に示します。
標準試料と検証用試料の混合比をそれぞれ表1,表2 に,それらの測定結果を図3(標準試料(1)~(5)),図4(標準試料(6)~(9)),図5(検証用試料(1)~(3))に示します。
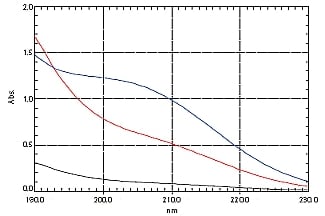
図2. ミネラルウォーターA,B,Cの吸収スペクトル
(赤:A,青:B,黒:C )
| A(%) | B(%) | C(%) | |
| 標準試料(1) | 20 | 30 | 50 |
| 標準試料(2) | 50 | 20 | 30 |
| 標準試料(3) | 30 | 50 | 20 |
| 標準試料(4) | 0 | 50 | 50 |
| 標準試料(5) | 50 | 0 | 50 |
| 標準試料(6) | 50 | 50 | 0 |
| 標準試料(7) | 100 | 0 | 0 |
| 標準試料(8) | 0 | 100 | 0 |
| 標準試料(9) | 0 | 0 | 100 |
| A(%) | B(%) | C(%) | |
| 検証用試料(1) | 10 | 80 | 10 |
| 検証用試料(2) | 30 | 30 | 40 |
| 検証用試料(3) | 20 | 60 | 20 |
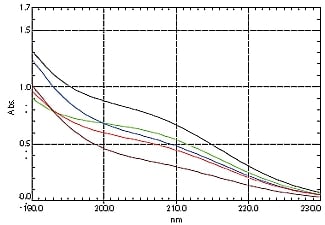
図3. 標準試料の吸収スペクトル
(その1: 標準試料(1)~(5))
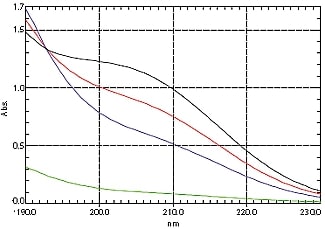
図4. 標準試料の吸収スペクトル
(その2: 標準試料(6)~(9))
4波長(200 nm,205 nm,210 nm,215 nm)の吸光度を用いて各ミネラルウォーターの検量モデル(重回帰式)を作成しました(3)。各モデルの重回帰式を表3 に示します。実測値と予測値(重回帰式から算出される値)との相関を示す重相関係数はA,B,C 各ミネラルウォーターのモデルでそれぞれ
(3) 表計算ソフトウェアExcel®を用いて計算しました。Excel®はMicrosoft社の商標または登録商標です。
| Aモデル | RA=1073.318・A200-1614.381・A205+1120.181・A210-731.675・A215-24.416 |
| Bモデル | RB=-541.210・A200+822.186・A205-91.882・A210-133.158・A215+3.725 |
| Cモデル | RC=-532.109・A200+792.195・A205-1028.299・A210+864.833・A215+120.690 |
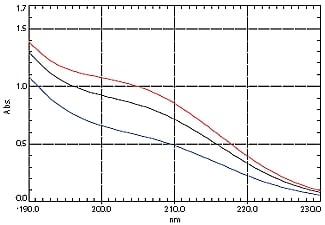
図5. 検証用試料の吸収スペクトル
(赤: (1),青: (2),黒: (3))
得られた重回帰式に検証用試料における4波長の吸光度を代入すると,各試料におけるミネラルウォーターの混合比が算出されます。定量結果を表4に示します。表2の値と比較すると良好な結果が得られていることがわかります。
多波長の吸光度を利用できる重回帰法は,今回の例のように多成分同時定量に威力を発揮します。
| A(%) | B(%) | C(%) | |
| 検証用試料(1) | 10.38 | 79.90 | 9.72 |
| 検証用試料(2) | 30.12 | 29.96 | 39.92 |
| 検証用試料(3) | 20.41 | 59.68 | 19.91 |
3. 主成分分析(PCA)を用いたミネラルウォーターの分類
次に主成分分析(PCA)を用いた事例を紹介します。ミネラルウォーター19種と水道水1種の計20種(A~T)の吸収スペクトルを図6~図8に分けて示します。
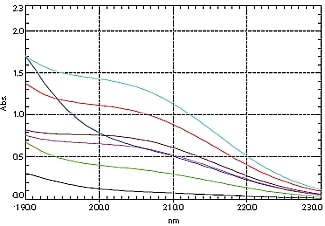
図6. ミネラルウォーターA~Gのスペクトル
(青:A,赤:B,黒:C,緑:D,茶:E,水色:F,紫:G)
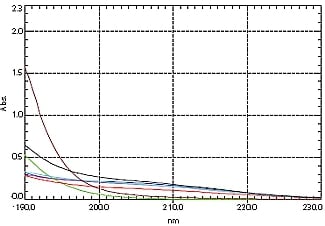
図7. ミネラルウォーターH~Nのスペクトル
(青:H,赤:I,黒:J,緑:K,茶:L,水色:M,紫:N)
取得した20本のスペクトルに対して主成分分析を行いました(4)。測定範囲190 nm~230 nmの全データを使用して解析しました。得られたスコアプロットを図9に示します。スコアプロットは第一主成分,第二主成分に対応するスコア(主成分得点)を座標表示したもので測定試料に対応する20点がグラフ上に表示されます。横軸は第一主成分に,縦軸は第二主成分に対応します。ここで“主成分”とは数学的に割り出されたなんらかの“特徴”を表します。近い点の試料は上記二つの主成分において,よく似た試料と言えます。図10において丸で囲ったグループ内にある試料のスペクトルを示します。グループ内のスペクトルはよく似ていることがわかります。
(4) 多変量解析ソフトウェア The Unscrambler®を用いて計算を行いました。The UnscramblerはCAMO社の商標または登録商標です。
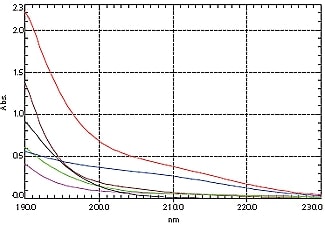
図8. ミネラルウォーターO~Sと水道水Tのスペクトル
(青:O,赤:P,黒:Q,緑:R,茶:S,紫:T [水道水] )
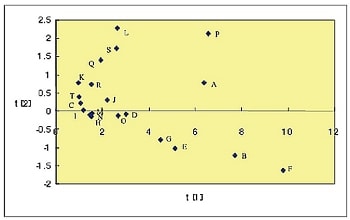
図9. スコアプロット
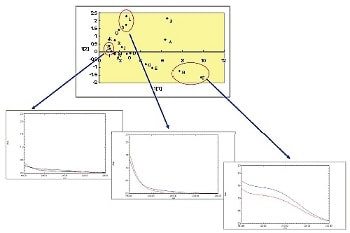
図10. スコアプロットにおける各グループの吸収スペクトル
(左から)C,I,Tのグループ,L,Sのグループ,B,Fのグループの吸収スペクトル
横軸(第一主成分)方向にプロット点を選択し対応するスペクトルを表示したものを図11に,縦軸(第二主成分)方向にプロット点を選択したものを図12に示します。これより,横軸は“総吸収量”(スペクトル面積)に関係し,縦軸は“スペクトル形状”(スペクトル中央付近における盛り上がりの有無)に関係していると推測されます(その推測が正しいことは,ローディングプロットというグラフを見ることによって確認できますが,詳細は略します)。“総吸収量”は試料に溶けているイオン等の総量に関係し,“スペクトル形状”はイオン等の種類に関係していると考えられます。このように主成分分析を用いることで多数の試料の類似度を視覚的に把握することが可能となります。
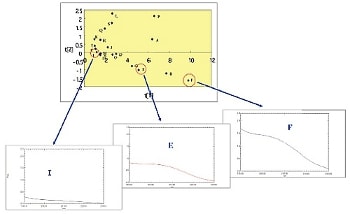
図11. スコアプロット: 横軸(第一主成分)に着目,抜き出したサンプル3つの吸収スペクトルの差異
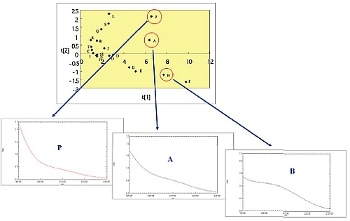
図12. スコアプロット: 縦軸(第二主成分)に着目,抜き出したサンプル3つの吸収スペクトルの差異
4. クラスター分析を用いたミネラルウォーターの分類
主成分分析(PCA)とは別の分類手法であるクラスター分析を用いると,よく似た試料同士を順にまとめていくデンドログラム(樹状図)で全試料を表示することができます。前述のミネラルウォーター20種に対し,クラスター分析を行った結果を図13に示します(5)。今回はWard 法という計算方法を用いてクラスター分析を行いました。図13 では主成分分析(PCA)のスコアプロットと合わせて表示しましたが,クラスター分析は主成分分析(PCA)とよく似た結果を与えていることがわかります。デンドログラムを見ることで,データやクラスターの類似度を把握することが可能となります。
(5) 多変量解析ソフトウェア The Unscrambler®を用いて計算を行いました。The UnscramblerはCAMO社の商標または登録商標です。
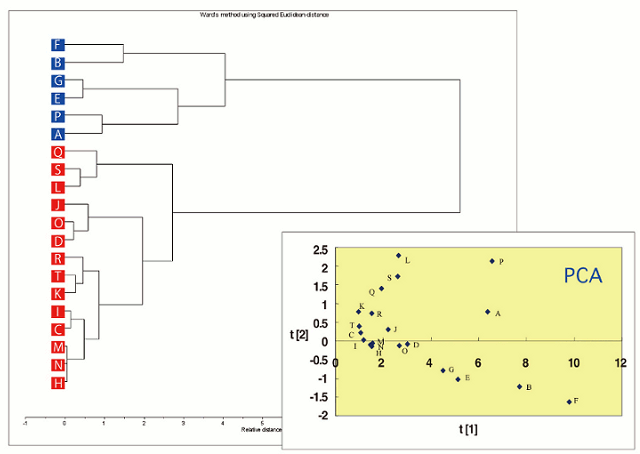
図13. クラスター分析結果とPCAスコアプロット
5. まとめ
今回,重回帰法を用いてミネラルウォーター3 種混合試料の同時定量を行うことができました。また主成分分析を用いてミネラルウォーター20 種をスコアプロット上で表現することができ,さらにクラスター分析を用いることによりデンドログラム(樹状図)にまとめることができました。分類手法を用いることで試料の類似度を視覚的に把握することが可能となります。
多変量解析は今回紹介した分析以外でも様々な場面で使われています。例えば,ミカン,リンゴなどの糖度や酸度を測定する簡易分光装置にも多変量解析が用いられています。その他,野菜の産地判別,においの分類,化粧品の効能評価,魚の脂肪量測定などその用途は様々です。また分野も食品,化学,ライフサイエンス,製薬,電気・半導体など多岐にわたります。分析データに対し多くの見方を提供する多変量解析は,今後も幅広く用いられていくことになると思われます。


