微粒子充てん剤
近年, 2μm程度に微粒子化された充てん剤を用いた超高速液体クロマトグラフが普及してきました。 充てん剤の微粒子化により,分離の向上や分離の高速化が期待できます。 ここでは,van Deemterの式を中心に微粒子充てん剤の持つ意味について解説します。
有効理論段高さ(H)とvan Deemterの式
ピークの分離の度合いを示す指標として理論段数 (N) が広く用いられています。 Nの値が大きいほどピークはシャープになり高分離を得ることができると考えられますが,Nの値はカラム長さ (L) にも比例して大きくなるため,“充てん剤として”の分離効率(性能)を示すことにはなりません。 このため,カラム長さによらず充てん剤としての分離効率を表す値として,カラム長さ (L) を理論段数 (N) で除した値,すなわち理論段一段あたりのカラム長さを示す理論段高さ (H) を用いて評価することが広く行われています。
式1で,Hが小さい,すなわちLは小さくNは大きい方が効率がよい充てん剤ということになりますが,さらに この理論段高さ(H)について,カラム充てん剤粒子径,移動相線速度などとの関係を示したvan Deemterの式 (式2)が広く知られています。
ここで,dpは充てん剤粒子径,vは移動相線速度です。 このvan Deemterの式は,3種類の独立した項目が理論段高さ(H)に寄与しているとして式が構成されています。 式2の第1項(A項)は,主に充てん剤粒子によって作られる多流路拡散に由来していると考えられ,充てん剤粒子径に比例します。 第2項(B項)は分子拡散に由来すると考えられ移動相線速度に反比例します。 また,第3項(C項)は物質移動に由来すると考えられ,粒子径の二乗と移動相線速度に比例します。 式2から,粒子径を小さくするとA項とC項が小さくなり,Hが小さくなることがわかります。
van Deemterカーブから見た充てん剤の微細化
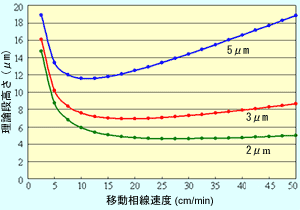
図1 充てん剤粒子径ごとのvan Deemter カーブ
van Deemterの式をプロットすると,図1のようなカーブが得られます。 このように充てん剤の粒子径を小さくしていくと,理論段高さ(H)が小さくなる,すなわち効率の高い充てん剤となることがわかります。 また,充てん剤粒子径を小さくすると,Hが最小になる線速度,すなわち最適な線速度が高くなることがわかります。
これは,充てん剤を微細化することにより,短いカラムで移動相流量を大きくしても分離を維持することが可能となることを意味します。 すなわち,分析の高速化が可能ということになります。
微粒子化充てん剤のメリットとデメリット
van Deemter式から考えると,充てん剤の微粒子化によりカラム効率は向上し,最適移動相線速度も向上するため高速化も可能ということになります。 しかし,微粒子充てん剤はこのようなメリットがある反面,カラムにおける圧力損失が大きくなるというデメリットがあります。
カラムにおける圧力損失は式3のように,移動相の粘性などの係数(ρ),カラム長さ(L)および,移動相線速度(v)に比例し,粒子径(dp)の二乗に反比例します。
このような背景から,5μm程度の充てん剤を用いた一般的なHPLCと同等の分離を行い,かつ分析時間を数分の一程度に短縮するために2μm程度の微粒子充てん剤が用いられるようになってきています。
しかし,装置の耐圧性能は向上してきたものの圧力には限界がありますし,消耗品の寿命にも影響します。 このため,圧力というデメリットを抑えながら高速化,高分離化のメリットを活用するためには,充てん剤粒子径を最適化する必要があります。


